Required Prior Knowledge
Questions
Complete the tables of values
| \(x\) | \(y\) |
|---|---|
| \(1\) | \(5\) |
| \(2\) | \(6\) |
| \(3\) | \(7\) |
| \(4\) | |
| \(5\) | |
| \(6\) | |
| \(10\) | |
| \(20\) | |
| \(17.2\) |
| \(x\) | \(y\) |
|---|---|
| \(1\) | \(20\) |
| \(2\) | \(17\) |
| \(3\) | \(14\) |
| \(4\) | |
| \(5\) | |
| \(6\) | |
| \(10\) | |
| \(-22\) | |
| \(-30\) |
Solutions
Notes
A relation is a set of ordered pairs. That is a set of coordinates.
Relations can be defined in various forms, such as by a:
list of coordinates;
algebraic rule;
table of values;
graph.
For some examples and non-examples of relations, see the video.
The domain of a relation is the set of all first values (\(x\) values) of the ordered pairs in a relation.
The range of a relation is the set of all second values (\(y\) values) of the ordered pairs in a relation.
Examples and Your Turns
Example
Find the domain and range of the relation given by$$\left\{\left(1,4\right),\left(2,7\right), \left(3,10\right), \left(4,13\right)\right\}$$
Your Turn
Find the domain and range of the relation given by$$\left\{\left(-2,4\right),\left(-1,1\right), \left(0,0\right), \left(1,1\right),\left(2,4\right)\right\}$$
Example
Find the domain and range of the relation given by
| \(x\) | \(y\) |
|---|---|
| \(3\) | \(5\) |
| \(2\) | \(2\) |
| \(3\) | \(7\) |
| \(4\) | \(6\) |
| \(1\) | \(7\) |
Your Turn
Find the domain and range of the relation given by
| \(x\) | \(y\) |
|---|---|
| \(16\) | \(4\) |
| \(16\) | \(-4\) |
| \(9\) | \(3\) |
| \(9\) | \(-3\) |
| \(4\) | \(2\) |
| \(4\) | \(-2\) |
Example
Find the domain and range of the relation given by$$A=\pi r^{2}$$
Your Turn
Find the domain and range of the relation given by$$x^{2}+y^{2}=1$$
Notes
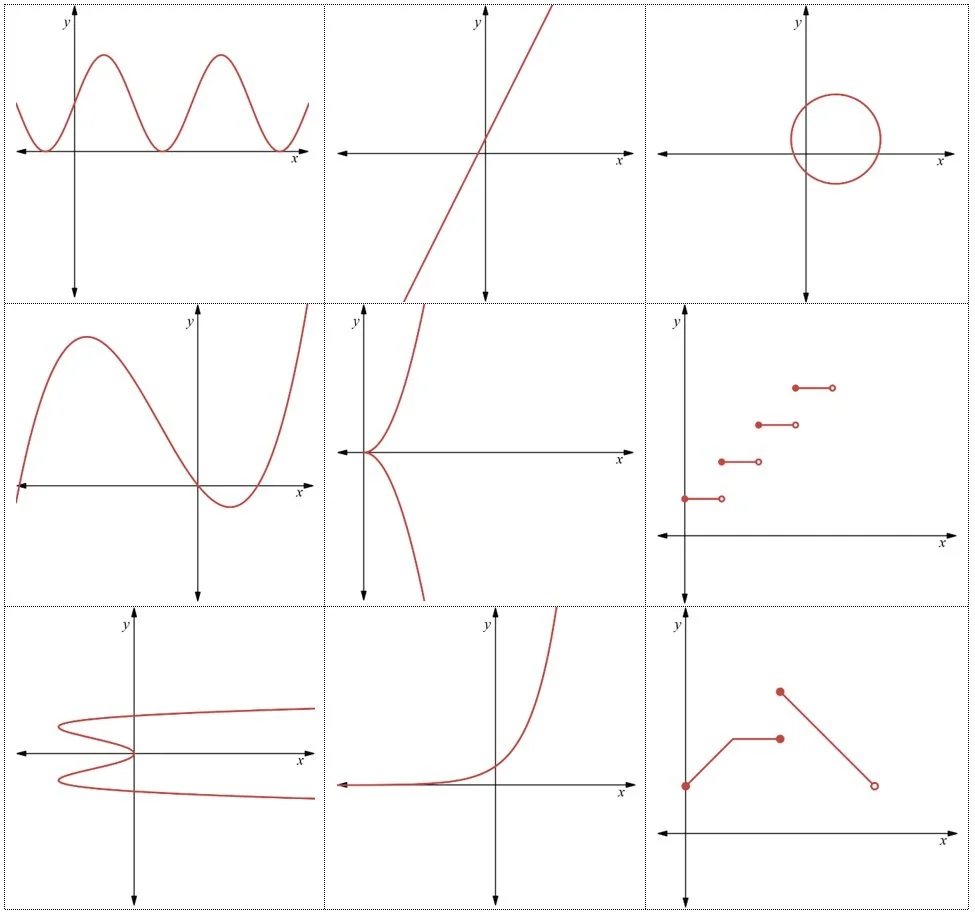
A function is a relation where each element of the domain maps to exactly one element of the range.
We can check this using the following methods:
In a function, no two ordered pairs have the same first element;
In a function, for each \(x\) value there is only one \(y\) value;
The graph of a function passes the Vertical Line Test - all possible vertical lines pass through the graph only once.
if any vertical line passes through the graph more than once, the graph does not show a function.
For some examples and non-examples of functions, see the video below.
When a function is graphed, we sometimes use the following notations:
An open circle \(\circ\) means the point is NOT included in the function
A closed circle \(\bullet\) means the point IS included in the function
An arrow \(\to\) on the end of a graph segment means the graph continues indefinitely in that direction.
Your Turn
Which of these are functions? Give a reason for your answer.
a) \(\left\{\left(5,5\right),\left(4,4\right),\left(3,3\right),\left(2,2\right),\left(1,1\right)\right\}\)
b) \(\left\{\left(-3,4\right),\left(-1,6\right),\left(0,5\right),\left(2,-1\right),\left(3,-1\right)\right\}\)
c) \(\left\{\left(4,1\right),\left(4,2\right),\left(4,3\right),\left(4,4\right),\left(4,5\right)\right\}\)
d) \(\left\{\left(-1,1\right),\left(0,3\right),\left(1,6\right),\left(2,8\right),\left(1,7\right)\right\}\)
e) \(\left\{\left(-4,4\right),\left(4,4\right),\left(-3,6\right),\left(3,6\right)\right\}\)
f) \(\left\{\left(1,2\right),\left(2,2\right),\left(3,2\right),\left(4,2\right),\left(5,1\right)\right\}\)
Your Turn
Which of these are functions? Give a reason for your answer.
Notes
There are four different types of relations.
See the video for definitions and examples of each.
Key Facts
Use this applet to generate a prompt for a Key Fact that you need to know for the course. The idea is that you should KNOW these key facts in order to be able to solve problems.
Taking it Deeper
Conceptual Questions to Consider
Why is it important that a function has only one output for each input? What would be the consequences if this were not the case?
Explain in your own words why the vertical line test works.
Can the range of a function be the same as the domain? Give an example.
What is the difference between a relation and a function? Is a function a relation? Is a relation a function?
Common Mistakes / Misconceptions
Confusing the domain and range of a relation.
Thinking that all equations represent a function (e.g. \(x^{2}+y^{2}=1\)).
Misunderstanding the vertical line test.
Connecting This to Other Skills
This skill is fundamentally important for the development of all other function-related skills covered in Unit 2.
A clear understanding of relations and functions is absolutely essential for success in calculus, which is explored in greater detail in Units 4 and 5.
Self-Reflection
What was the most challenging part of this skill for you?
What are you still unsure about that you need to review?