Unit 1 - Number and Algebra
Required Prior Knowledge
Questions
Expand and simplify
a) \(\left(a+b\right)^{1}\)
b) \(\left(a+b\right)^{2}\)
c) \(\left(a+b\right)^{3}\)
d) \(\left(a+b\right)^{4}\)
e) \(\left(a+b\right)^{5}\)
f) \(\left(a+b\right)^{6}\)
Solutions
Get Ready
Questions
Looking at your answers to the Required Prior Knowledge:
What do you notice?
What do you wonder?
Make a conjecture
Predict the expansion for \(\left(a+b\right)^{7}\)
Predict the expansion for \(\left(a+b\right)^{10}\)
Solutions
Notes
A binomial is an expression of the form \(\left(a+b\right)\).
Examples of binomials$$2x+7\\17-5a\\2x+\frac{1}{2}y\\3n^{2}-\frac{2}{n}\\3x+\left(y+1\right)$$
Non-Examples of binomials$$4x\\2x^{2}-x+2$$
Binomial expansion is when we expand powers of binomials.
For the binomial expansion of \(\left(a+b\right)^{n}\) where \(n\in\mathbb{N}\)
The power of \(a\) in the leading term is \(n\)
The powers of \(a\) decrease by 1 each term
The power of \(b\) in the leading term is \(0\)
The powers of \(b\) increase by 1 each term
The sum of the powers of \(a\) and \(b\) in any term is \(n\)
The number of terms in the expansion is \(n+1\)
The coefficients of each term come from Pascal’s Triangle
Pascal’s Triangle begins with 1 and each term is the sum of the two numbers above it. The first few rows are shown below.$$ 1\\ 1\quad 1\\ 1\quad 2\quad 1\\ 1\quad 3\quad 3\quad 1\\ 1\quad 4\quad 6\quad 4\quad 1\\ 1\quad 5 \quad 10\quad 10 \quad 5\quad 1\\ 1\quad 6 \quad 15\quad 20 \quad 15\quad 6 \quad 1$$We choose the row from Pascal’s Triangle where the first non-one number is the power \(n\) of the binomial.
Each term of a binomial is thus made up of three parts:
Pascal’s coefficient
A descending power of \(a\)
An ascending power of \(b\)
We can lay this out in a tabular arrangement to help see the different parts of the expansion.
Consider the expansion of \(\left(x+1\right)^{4}\).$$\begin{matrix}\text{pascal row}&1&4&6&4&1\\ \text{powers of }a&x^{4}&x^{3}&x^{2}&x^{1}&x^{0}\\ \text{powers of }b&1^{0}&1^{1}&1^{2}&1^{3}&1^{4}\end{matrix}$$We then multiply down each column to get each term, giving$$\left(x+1\right)^{4}=x^{4}+4x^{3}+6x^{2}+4x+1$$
Examples and Your Turns
Example
Expand$$\left(2+3x\right)^{5}$$
Your Turn
Expand$$\left(3-2x\right)^{6}$$
Your Turn
Expand$$\left(2y+3x\right)^{5}$$
Your Turn
Expand$$\left(2y-3x\right)^{5}$$
Your Turn
Expand$$\left(1+\frac{1}{x}\right)^{4}$$
Your Turn
Expand$$\left(1+\frac{2}{x}\right)^{4}$$
Your Turn
Expand$$\left(x-\frac{1}{x}\right)^{5}$$
Your Turn
Expand$$\left(x-\frac{1}{x}\right)^{6}$$
Your Turn
Expand$$\left(x^{2}-\frac{1}{2x}\right)^{5}$$
Your Turn
Expand$$\left(x^{2}-\frac{2}{x^{3}}\right)^{6}$$
Notes
When the power of the binomial gets large, it becomes time consuming to find the Pascal coefficient using the triangle.
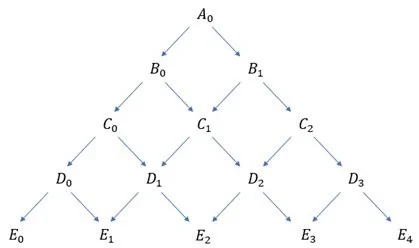
Consider the triangle in the image below.
Determine how many ways there are to get to each of the labelled points from \(A_{0}\), given that you can only travel in the direction of an arrow.
You should notice that these values give Pascal’s Triangle.
Now consider the expansion of \(\left(a+b\right)^{4}=\left(a+b\right)\left(a+b\right)\left(a+b\right)\left(a+b\right)\), without simplifying by collecting like terms.
Which combinations of products would give us a term of the form \(a^{2}b^{2}\)?
How does this compare to the value in Pascal’s Triangle in position \(E_{2}\)
Explain why this is given by \(\binom{4}{2}\).
This means we can rewrite Pascal’s Triangle in terms of combinations as below$$ \binom{0}{0}\\ \binom{1}{0}\quad \binom{1}{1}\\ \binom{2}{0}\quad \binom{2}{1}\quad \binom{2}{2}\\ \binom{3}{0}\quad \binom{3}{1}\quad \binom{3}{2}\quad \binom{3}{3}\\ \binom{4}{0}\quad \binom{4}{1}\quad \binom{4}{2}\quad \binom{4}{3}\quad \binom{4}{4}$$where \(\binom{n}{r}\) gives us the \(r\)th element of the \(n\)th row of Pascal’s Triangle.
Using the values from Pascal’s Triangle state the value of
(a) \(\binom{5}{1}\)
(b) \(\binom{5}{3}\)
(c) \(\binom{6}{3}\)
-
a) \(\binom{5}{1}=5\)
b) \(\binom{5}{3}=10\)
c) \(\binom{6}{3}=20\)
From our work on Combinations, we know that$$\binom{n}{r}=\frac{n!}{r!\left(n-r\right)!}$$We can use this to find values of larger binomial coefficients.
Examples and Your Turns
Example
Calculate the value of \({}^{10} \mathrm{ C }_{3}\).
Your Turn
Calculate the value of \(\binom{11}{9}\).
Example
Determine the eighth term of the expansion of$$\left(2x+\frac{1}{x}\right)^{12}$$
Your Turn
Determine the seventh term of the expansion of$$\left(3x-\frac{4}{x^{2}}\right)^{12}$$
Example
Determine the term containing \(a^{3}\) in the expansion of$$\left(2a-3b\right)^{9}$$
Your Turn
Determine the term containing \(x^{8}\) in the expansion of$$\left(4x-y\right)^{12}$$
Example
Determine the term independent of \(x\) in the expansion of$$\left(3x^{2}-\frac{1}{2x}\right)^{9}$$
Your Turn
Determine the term independent of \(x\) in the expansion of$$\left(3x-\frac{1}{2x^{2}}\right)^{12}$$
Your Turn
Determine the term independent of \(x\) in the expansion of$$\left(4x^{3}-\frac{2}{x^{2}}\right)^{5}$$
Your Turn
Find the values of \(a, b\) and \(c\) in$$\left(1+2x\right)^{8}\equiv 1+ax+bx^{2}+cx^{3}+…+256x^{8}$$
Your Turn
Find the values of \(a, b\) and \(c\) in$$\left(1+\frac{x}{2}\right)^{a}\equiv 1+bx+cx^{2}+…+\left(\frac{x}{2}\right)^{10}$$
Your Turn
Find the values of \(a, b\) and \(c\) in$$\left(2-ax\right)^{6}\equiv b-64x+cx^{2}+cx^{3}+…$$
Example
Given that the coefficient of \(x^{3}\) in the expansion of \(\left(1+kx\right)^{10}\) is \(15\), calculate the value of the constant \(k\).
Your Turn
Given that the coefficient of \(x^{2}\) in the expansion of \(\left(1+qx\right)^{8}\) is \(112\), calculate the value of the constant \(q\).
Example
Find the coefficient of \(x^{5}\) in the expansion of$$\left(x+3\right)\left(2x-1\right)^{6}$$
Your Turn
Find the coefficient of \(x^{2}\) in the expansion of$$\left(x-1\right)\left(2-3x\right)^{5}$$
Your Turn
The coefficient of \(x^{5}\) in the expansion of \(\left(\frac{2}{ax}+ax\right)^{7}\) is \(3402\). Calculate the value of \(a\).
Key Facts
Use this applet to generate a prompt for a Key Fact that you need to know for the course. The idea is that you should KNOW these key facts in order to be able to solve problems.