Required Prior Knowledge

Questions

List the different transformations you know, and the information required to perform each of them.

Solutions

Get Ready

Questions

Use the desmos activity below to investigate the following. You may choose which function to use in order to investigate; I would recommend $f\left(x\right)=x^{3}-5x-1$ which is already in the activity (you can edit it if you wish).

Task 1

Open the folder for Task 1.

Describe the effects of the following transformations using mathematical vocabulary.

$y=f\left(x\right)+k$
$y=f\left(x+k\right)$

These transformations are both ____________________

Practice

Describe the transformation that takes $y=f\left(x\right)$ to:

a) $ y=f\left(x+8\right)+1$

b) $y=f\left(x-3\right)+5$

c) $y=f\left(x-1\right)-6$

Write the equations of the graphs when we translate $y=f\left(x\right)$ by the vector:

d) $\begin{pmatrix}1\\3\end{pmatrix}$

e) $\begin{pmatrix}-2\\4\end{pmatrix}$

f) $\begin{pmatrix}a\\b\end{pmatrix}$

Task 2

Hide the graphs in Task 1, close the Task 1 folder and open the Task 2 folder.

Describe the effects of the following transformations using mathematical vocabulary:

$y=-f\left(x\right)$
$y=f\left(-x\right)$

These transformations are both ____________________

Extension

Can you describe the single transformation given by the graph of $y=-f\left(-x\right)$.

Task 3

Hide the graphs in Task 2, close the Task 2 folder and open the Task 3 folder.

Describe the effects of the following transformations using mathematical vocabulary:

$y=af\left(x\right)$
$y=f\left(ax\right)$

These transformations are both _________________________

Notes

A transformation is a rule which when applied to a geometric shape, produces an image of the figure with each point changed in a given way.

We will be looking at the transformation of functions and how they change the function algebraically.

A Translation is a transformation where every point in the image is moved the same distance in the same direction.

A translation can be horizontal, vertical, or a combination of both.

This is usually described using a vector in the form $\begin{pmatrix}h\\k\end{pmatrix}$ where $h$ is the horizontal movement (when $h$ is positive the movement is to the right) and $k$ is the vertical movement (when $k$ is positive the movement is upwards).

When the graph of the function $y=f\left(x\right)$ is translated by $\begin{pmatrix}h\\k\end{pmatrix}$, the resulting functions has the equation $$y=f\left(x-h\right)+k$$

Examples and Your Turns

Example

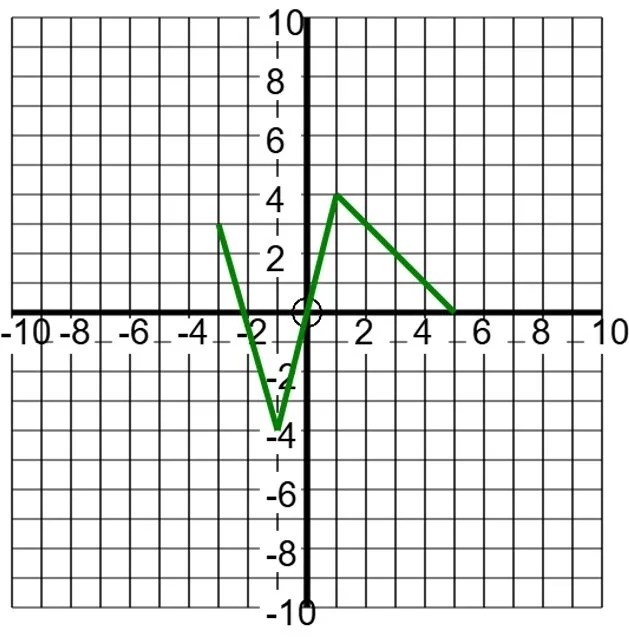
Shown is the graph of $y=f\left(x\right)$. Draw the graph of $y=f\left(x+1\right)-4$.

The graph of a function made up of straight line segments.

Your Turn

Shown is the graph of $y=h\left(x\right)$. Draw the graph of $y=h\left(x-5\right)-3$.

Your Turn

Shown is the graph of $y=f\left(x\right)$. Draw the graph of $y=f\left(x-4\right)+5$.

Your Turn

Shown is the graph of $y=g\left(x\right)$. Draw the graph of $y=g\left(x+3\right)+2$.

Example

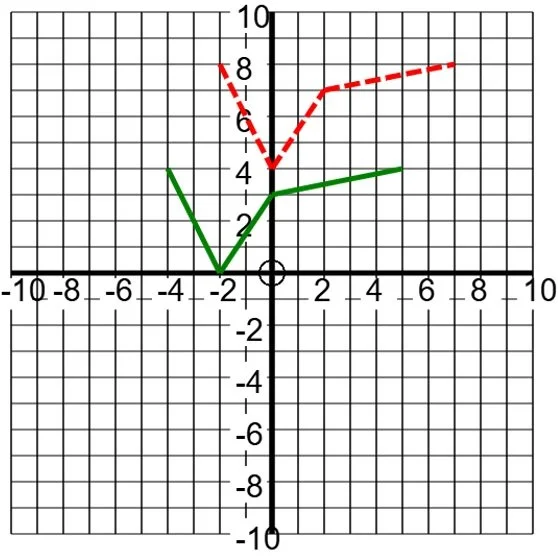
Shown is the graph of $y=p\left(x\right)$ with a solid green line. What is the equation of the graph with the dashed red line?

Your Turn

Shown is the graph of $y=f\left(x\right)$ with a solid green line. What is the equation of the graph with the dashed red line?

Your Turn

Shown is the graph of $y=g\left(x\right)$ with a solid green line. What is the equation of the graph with the dashed red line?

Your Turn

Shown is the graph of $y=f\left(x\right)$ with a solid green line. What is the equation of the graph with the dashed red line?

Notes

A stretch is a transformation where each point’s distance from an invariant line is multiplied by a factor.

The points can get further from the invariant line or closer to it.

When the graph of the function $y=f\left(x\right)$ is stretched by a factor of $a$ with invariant line the $x$-axis (a vertical stretch) the resulting function has equation$$y=af\left(x\right)$$When the graph of the function $y=f\left(x\right)$ is stretched by a factor of $b$ with invariant line the $y$-axis (a horizontal stretch) the resulting function has equation$$y=f\left(\frac{1}{b}x\right)$$

Examples and Your Turns

Example

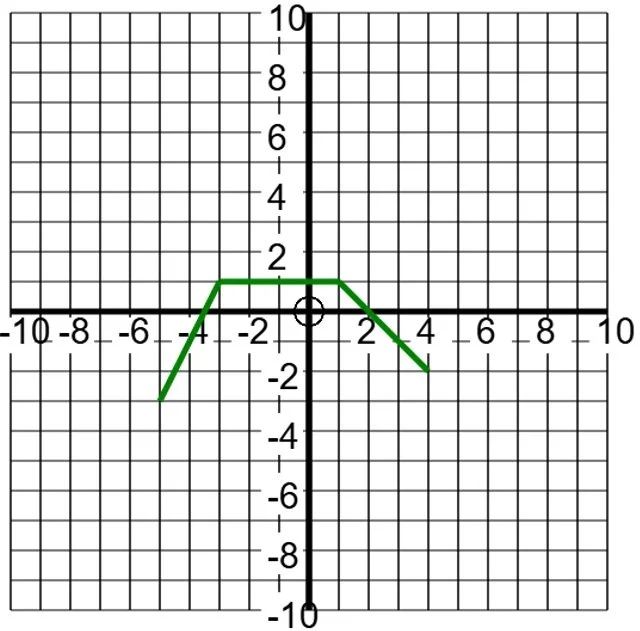
Shown is the graph of $y=f\left(x\right)$. Draw the graph of $y=2f\left(x\right)$.

Your Turn

Shown is the graph of $y=h\left(x\right)$. Draw the graph of $y=3h\left(x\right)$.

Your Turn

Shown is the graph of $y=f\left(x\right)$. Draw the graph of $y=\frac{1}{3}f\left(x\right)$.

Your Turn

Shown is the graph of $y=g\left(x\right)$. Draw the graph of $y=\frac{1}{4}g\left(x\right)$.

Example

Shown is the graph of $y=f\left(x\right)$. Draw the graph of $y=f\left(3x\right)$.

Your Turn

Shown is the graph of $y=h\left(x\right)$. Draw the graph of $y=h\left(4x\right)$.

Your Turn

Shown is the graph of $y=f\left(x\right)$. Draw the graph of $y=f\left(\frac{1}{4}x\right)$.

Your Turn

Shown is the graph of $y=h\left(x\right)$. Draw the graph of $y=h\left(\frac{1}{2}x\right)$.

Example

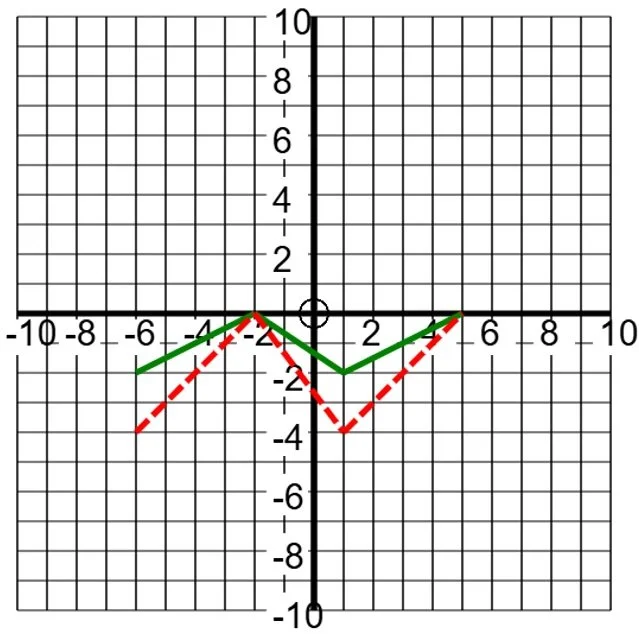
Shown is the graph of $y=p\left(x\right)$ with a solid green line. What is the equation of the graph with the dashed red line?

Your Turn

Shown is the graph of $y=f\left(x\right)$ with a solid green line. What is the equation of the graph with the dashed red line?

Your Turn

Shown is the graph of $y=p\left(x\right)$ with a solid green line. What is the equation of the graph with the dashed red line?

Your Turn

Shown is the graph of $y=f\left(x\right)$ with a solid green line. What is the equation of the graph with the dashed red line?

Notes

A reflection is a transformations which creates a mirror image across a line of symmetry. Each point on the image remains the same distance from this line, but on the opposite side.

When the graph of the function $y=f\left(x\right)$ is reflected in the $x$-axis (vertical direction) the resulting function has equation $$y=-f\left(x\right)$$When the graph of the function $y=f\left(x\right)$ is reflected in the $y$-axis (horizontal direction) the resulting function has equation $$y=f\left(-x\right)$$Note that reflections are a special case of stretches when the factor is equal to $-1$.

Examples and Your Turns

Your Turn

Shown is the graph of $y=h\left(x\right)$. Draw the graph of $y=-h\left(x\right)$.

Your Turn

Shown is the graph of $y=h\left(x\right)$. Draw the graph of $y=h\left(-x\right)$.

Investigation

Use the desmos activity below to:

Describe the transformations, in particular the order in which they happen, for $y=f\left(2x+3\right)$;
Describe the transformations, in particular the order in which they happen, for $y=f\left(2\left(x+3\right)\right)$;

What do you notice? Are they the same?

Did the order surprise you?

Notes

When listing transformations for the usual form $$y=af\left(b\left(x-h\right)\right)+k$$translations should be listed AFTER stretches and reflections.

If a function is given in the form $f\left(bx-h\right)$, then it is best to factorise it first to be in the form $f\left(b\left(x-\frac{h}{b}\right)\right)$ so we can apply stretched first, then translations.

In general it is useful to remember the following:

You need to be able to do the following in the A&A HL course:

Given a graph of $y=f\left(x\right)$, draw the graph of $y=af\left(b\left(x+c\right)\right)+d$;
Given a function in the form $y=af\left(b\left(x+c\right)\right)+d$, or alternate forms, list the transformations from $y=f\left(x\right)$;
Given a list of transformation of $y=f\left(x\right)$, write the resulting function.

Examples and Your Turns

Example

The function $y=f\left(x\right)$ is transformed into$$y=2f\left(3\left(x+1\right)\right)-4$$List the transformations that have occurred in order.

Your Turn

The function $y=f\left(x\right)$ is transformed into$$y=-3f\left(\frac{1}{4}\left(x-2\right)\right)+1$$List the transformations that have occurred in order.

Your Turn

The function $y=f\left(x\right)$ is transformed into$$y=\frac{1}{5}f\left(-\left(x+2\right)\right)+7$$List the transformations that have occurred in order.

Your Turn

The function $y=f\left(x\right)$ is transformed into$$y=3f\left(-\frac{1}{2}\left(x-5\right)\right)-1$$List the transformations that have occurred in order.